My logging file gets too big! — Python logging to multiple files

My log file gets too large! — Python logging to multiple files

After a few weeks of logging that poor single logging file becomes pretty huge. In this short and simple article we’ll create a special file handler that writes to a file until a certain file size is exceeded. Then it stores the file and writes the logs to a new one. Let’s code!

There are two strategies for determining when to write to a new file: based on the file size and based on time. First we’ll check out the rotating file handler, then the timed rotating file handler.

1. RotatingFileHandler

This handler writes to a file until it has reached a set size in bytes. Check out the sample below:

When we run this code we see the following in out logdir:

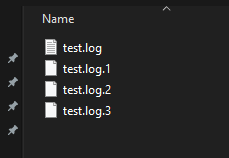
What happens when the file size exceeds the set limit?
The example above will save all logs to a file called test.log. If that file is full (if its size is 100KB) then test.log will be renamed to test.log.1 and a new test.log will be created. If test.log.1 already exitsts it will be renamed to test.log.2 etc. Also we’ve specified (with backupCount=3) that we don’t want a test.log.4; these files get deleted.

Keep your code secure by using environment variables and env files

Securely load a file containing all of our app’s required, confidential data like passwords, tokens, etc

2. TimedRotatingFileHandler

This handler doesn’t look at the file size as the RotatingFileHandler but rolls over to a new file according to a specified time interval that we can specify with the when and interval parameters:

Now the logger creates a new logfile every 3 seconds, as specified by the when and interval. Since we sleep every second, and our interval is every 3 seconds, the code above creates two files; the first one for the first 3 seconds, the last one for the remaining one.

When can be specified with s(econds), m(inute), h(our), d(ay), w0 — w6 (where w0 is monday) and midnight.

Safely test and apply changes to your database: getting started with Alembic

Version control your database with this simple Python tool

Conclusion

This article was a quick follow-up on this one about file handlers.

I hope everything was as clear as I hope it to be but if this is not the case please let me know what I can do to clarify further. In the meantime, check out my other articles on all kinds of programming-related topics like these:

• Cython for absolute beginners — 30x faster code in two simple steps
• Why Python is so slow and how to speed it up
• Git for absolute beginners: understanding Git with the help of a video game
• Simple trick to work with relative paths in Python
• Docker for absolute beginners: the difference between an image and a container
• Docker for absolute beginners — what is Docker and how to use it (+ examples)
• Virtual environments for absolute beginners — what is it and how to create one (+ examples)
• Create and publish your own Python package
• Create a fast auto-documented, maintainable, and easy-to-use Python API in 5 lines of code with FastAPI

Happy coding!

— Mike

P.S: like what I’m doing? Follow me!

Join Medium with my referral link — Mike Huls

As a Medium member, a portion of your membership fee goes to writers you read, and you get full access to every story…